We have already studied the triangle and also the types of a triangle in Previous classes. Here we will discuss a particular type of triangle i.e. right-angled triangle. Let us take some examples where we use a right-angled triangle:
- If you go to Delhi to visit the Qutub Minar so you can find out the height of this one without actual measurement with the help of a right angle triangle.
- A student standing on a balcony and watching the kite which is flying in the sky hence between the kite and that student’s eyes a right-angle triangle formed.
In the above example we can find out the height or distance in a specific branch of mathematics, that specific branch is called trigonometry.
What is Trigonometry?
It is a mixed form of some greek words,

Tri + gono+metron = trigonometry
- Tri = three
- gon = sides
- metron = measurement
It means the measurement of three sides, hence in trigonometry, we will study the relationship between the sides and angles of a right-angled triangle.
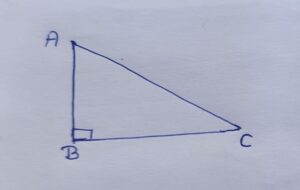
Here,
∠B = right angle = 90°
∠A and∠C both are acute angles, Here in the Right angled triangle we will measure these acute angles in the form of the ratio of sides.

(AC)2 = (AB)2 + (BC)2
In a right-angled triangle, the square of the largest side (AC) is equal to the square of some of the remaining two sides(BC and AB) This is called the Pythagoras theorem (p.g.t.)Or Bodhayan theorem
Here are some examples based on P.G.T. theorem:
Q1. In triangle ABC right-angled at B, AB = 24cm, BC = 7cm Find AC…..?
Given:
In Triangle ABC

∠B = 90º
AB = 24cm
BC = 7cm
To Find:
AC = ?
Solution:
In triangle ABC
By P.G.T. (Pythagoras Theorem)
(AC)2 = (AB)2 + (BC)2
=> (AC)2 = (24)2 + (7)2
=> (AC)2 = 576 + 49
=> (AC)2 = 625
=> AC = √625
=> AC = 25
Q2. Consider triangle ACB, right-angled at C, in Which AB = 29 units, BC = 21units Then Find AC….?
Given:
In triangle ABC

∠C = 90°
AB = 29 units
BC = 21 units
To Find:
AC = ?
Solution:
In triangle ABC
By P.G.T.
(AB)2 = (AC )2 + (BC)2
=> (29)2 = (AC )2 + (21)2
=> 841 = (AC )2 + 441
=> 841 – 441 = (AC )2
=> √400 = (AC)
=> 20 = AC
What is Trigonometry Ratio
There are six ratios of trigonometry.

Sine of θ = Side of the opposite angle of θ/Hypotenus (H) = P/H = sinθ
Cosine of θ = Side of the adjacent angle of θ/Hypotenus (H) = b/H = cosθ
Tangent of θ = Side of the opposite angle of θ/ Side of the adjacent angle of θ = P/b = tanθ
Cotangent of θ = 1/Tangent of θ=Side of adjacent to θ/side opposite to θ = b/P = cotθ
Secant of θ = 1/Cosine of θ = H/Side of Adjacent to θ = H/b = secθ
Cosecant of θ = 1/sine of θ = H/side of opposite to θ = H/P = cosecθ

Some practice questions based on trigonometric ratios.
Q1. In triangle ABC right-angled at B, AB = 24cm, BC = 7cm. Determine:
(i) All trigonometry ratios for angle ∠A
Or
sinA, cos A, tanA, cotA, secA, cosecA
(ii) All Trigonometry ratios for ∠C
or
sinC, cosC, tanC, cotC, secC, cosecC
Given:
in Triangle ABC

∠B = 90º
AB = 24cm
BC = 7cm
To Find:
(i) All trigonometry ratios for angle ∠A
Or
sinA, cos A, tanA, cotA, secA, cosecA
(ii) All Trigonometry ratios for ∠C
or
sinC, cosC, tanC, cotC, secC, cosecC
Solution:
In triangle ABC
By P.G.T. (Pythagoras Theorem)
(AC)2 = (AB)2 + (BC)2
=> (AC)2 = (24)2 + (7)2
=> ( AC)2 = 576 + 49
=> (AC)2 = 625
=> AC = √625
=> AC = 25
For angle ∠A

P = Perpendicular =7
b = base = 24
H = Hypotenus = 25
sinA = P/H = 7/25
cosA = b/H = 24/25
tanA = P/b = 7/24
CotA = b/P = 24/7
SecA = H/b = 25/24
cosecA = H/P = 25/7
For angle ∠C
P = 24
b = 7
H = 25
sinC = P/H = 24/25
CosC = b/H = 7/25
tanC = P/b = 24/7
cotC = b/p = 7/24
secC = H/b = 25/7
cosecC = H/P = 25/24
Q2. Consider triangle ACB, right-angled at C, in Which AB = 29 units, BC = 21 units and ∠ABC = θ Determine The Value of
(i) cos2θ + sin2θ
(ii) cos2θ – sin2θ
(iii) sec2θ – tan2θ
(iv) cosec2θ – cot2θ
Given
In triangle ABC

∠C = 90°
AB = 29 units
BC = 21 units
∠ABC = θ
To Find:
(i) cos2θ + sin2θ
(ii) cos2θ – sin2θ
(iii) sec2θ – tan2θ
(iv) cosec2θ – cot2θ
Solution:
In triangle ABC
By P.G.T.
(AB)2 = (AC)2 + (BC)2
=> (29)2 = (AC)2 + (21)2
=> 841 = (AC)2 + 441
=> 841 – 441 = (AC)2
=> √400 = (AC)
=> 20 = AC
For √ABC = θ
P = 20
b = 21
H = 29
sinθ = P/H = 20/29
cosθ = b/H = 21/29
tanθ = P/b = 20/21
cotθ = b/P = 21/20
secθ = H/b = 29/21
cosecθ = H/p = 29/20
(i) cos2θ + sin2θ
=> (21/29)2 + (20/29)2
=> 441/841 + 400/841
=> (441 + 400)/841
=> (841)/841
=> 1
(ii) cos2θ – sin2θ
=> (21/29)2 – (20/29)2
=> 441/841 – 400/841
=> (441 – 400)/841
=> 0/841
=> 0
(iii) sec2θ – tan2θ
=> (29/21)2 – ( 20/21)2
=> 841/441 – 400/441
=> (441 )/441
=> 1
(iv) cosec2θ – cot2θ
=> (iv) (29/20)2 – ( 21/20)2
=> 841/400 – 441/400
=> (841 – 441)/400
=> 400/400
=> 1
If you have any queries related to Trigonometry and Trigonometric Ratios you can ask in the comment section below.
