Theorem 6.1 Thale’s Theorem/ Basic Proportionality Theorem (BPT)
Statement: ” If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points. The other two sides are divided in the same ratio.”
OR
Prove that in a triangle a line parallel to one side divides remaining two sides in the same ratio
Given:
In Δ ABC
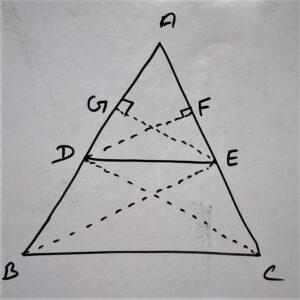
DE // ( parallel to ) BC
To Prove:
AD/BD = AE/CE
Construction:
DF ⊥ ( Perpendicular ) on AC
EG ⊥ ( Perpendicular ) on AB
Join B to E and C to D
Proof:
According to figure:
In Δ ADE and Δ BDE

have common altitude (Perpendicular) = EG
∴ area Δ ADE /area Δ BDE = 1/2×b×h / 1/2×b×h
⇒ area Δ ADE /area Δ BDE = AD×EG / BD×EG
⇒ area Δ ADE /area Δ BDE = AD / BD ————-equation (i)
Similarly
In Δ ADE and Δ CED
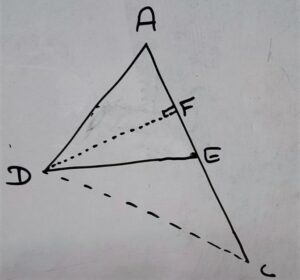
Have common altitude(perpendicular) = DF
ar Δ ADE / ar Δ CED = 1/2×b×h / 1/2×b×h
⇒ ar Δ ADE / ar Δ CED = AE×DF / CE×DF
⇒ ar Δ ADE / ar Δ CED = AE / CE ————-equation (ii)
Δ BDE and Δ CED are lies on Common base (DE) and between same parallel lines
∴ ar Δ BDE = ar Δ CED
Dividing both side by area Δ ADE
⇒ ar Δ BDE/ar Δ ADE = ar Δ CED/ar Δ ADE
⇒ ar Δ ADE/ar Δ BDE = ar Δ ADE/ar Δ CED [ After reciprocal of both side] ————–equation(iii)
By comparing equation (i) and equation(ii) with equation (iii) We get
AD/BD = AE/CE Hence proved
